
工程能力 VS 工程性能
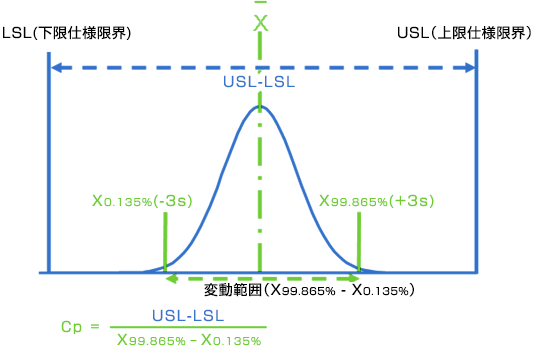
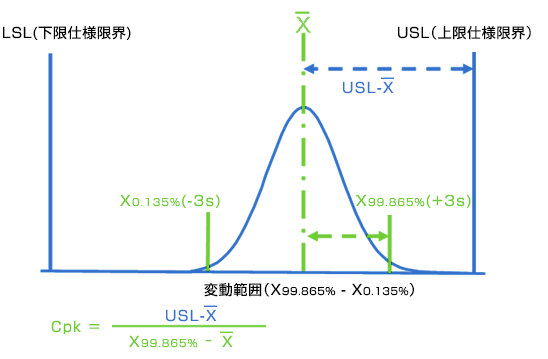
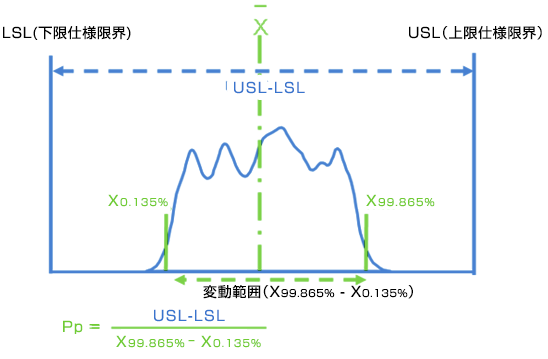
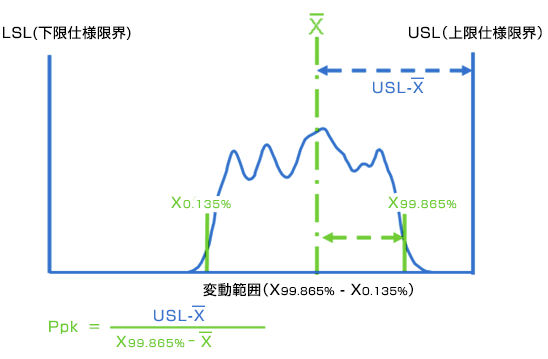
工程能力を確立する、すなわち工程能力指数Cp、Cpkを計算する場合は、99.73%の特性値変動範囲(正規分布の変動範囲±3σに相当する)に着目し、これが基準変化量となります。ISO 22514-2では、計算方法としてパーセンタイル法を推奨しています。
この規格には様々な時間依存分布モデルがあり、この中から測定されたデータの分布に最適な分布モデルを選択します。
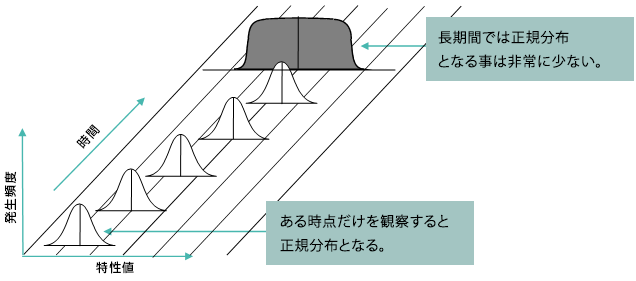
工程能力は、分布の位置と、分布範囲の分布の平均値パラメータが安定している場合にのみ確立されます。
しかし、現実的にはほとんどの工程が、この要件を長期間に亘り満たすことができません。
これが、ISO 22514-2で工程能力と工程性能を区別している理由です。
分布範囲と分布平均値パラメータが不安定な場合、工程能力指数CpとCpkの代わりに、工程性能指数Pp、Ppkを使用すると規定されています。しかし企業ガイドラインの中には、予備的工程能力を示すために能力指数Pp、Ppkを使用していることがあったり、Tp、Tpkを一時的な能力指数として適用されることもあります。
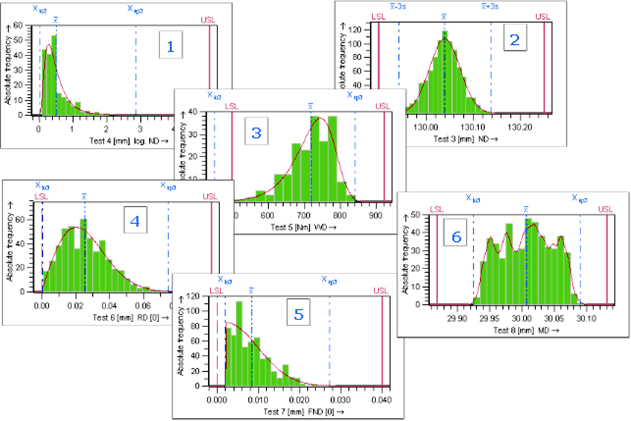
Q-DASのソフトウェアはデータの分布から、最適な分布モデル選択し、Cp、CpkやPp、Ppkの値を自動算出してくれます。また、確率プロットや、累積曲線のグラフを使用して分布モデルが実際の数値分布を正しく表しているか確認する事が可能です。
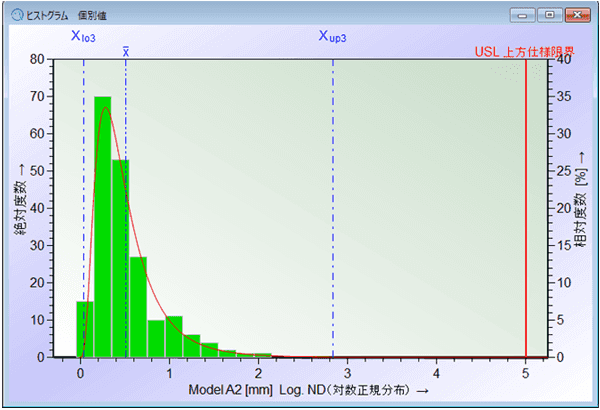
下図は平面度のデータです。平面度は0が下方の自然限界となる(0以下にならない)ので、データの分布は左右非対称となります。
正規分布を当てはめ、確率プロットを見ると値が正規分布していない事が分かります。このデータの場合、対数正規分布が最もデータの分布を表すのに適切なモデルとして選択されました。確率プロットを見ると、分布モデルのラインに沿ってデータが存在している事を確認できます。
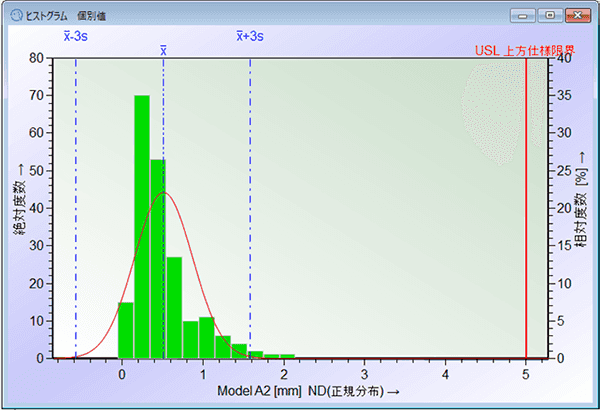

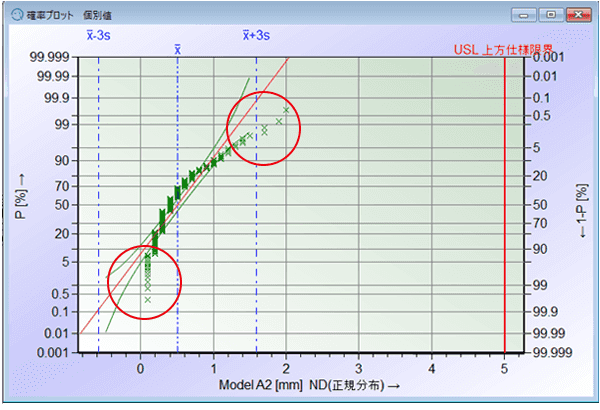
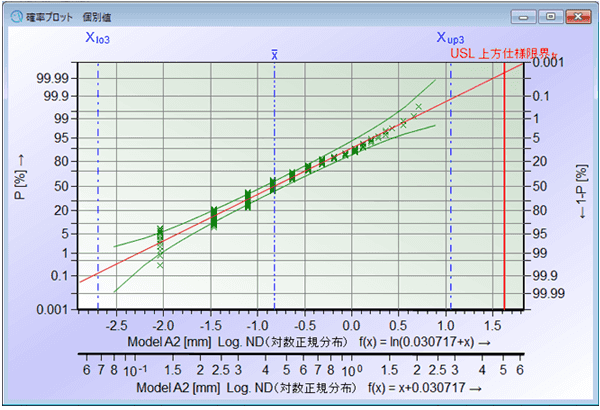
このように適切な分布モデルを使用する事で、Cp、Cpk、Pp、Ppkに必要となる99.73%の特性値変動範囲を正確に求める事が出来るため、正規分布しない工程でも規格に準拠した工程能力、工程性能評価が可能となります。